. Тригональная сингония включает все кристаллы, имеющие одну тройную ось.
Гексагональная сингония включает все кристаллы, имеющие одну гексагональную ось (ось 6-го порядка).
Тетрагональная сингония включает все кристаллы, имеющие одну четверную (тетрагональную) ось (ось 4-го порядка).
Кубическая (правильная, изометрическая) сингония включает все кристаллы, имеющие четыре тройные и три четверные оси. Тройные оси параллельны диагоналям куба и наклонены одна к другой под углом 70°32.
(Иногда тригональная сингония считается частью гексагональной сингонии, так что в этом случае насчитывается всего шесть различных сингоний.).
Кристаллы различных сингоний (систем) в свою очередь делятся на виды (классы) симметрии по совокупности элементов симметрии, которые дополняют характерные элементы сингонии, указанные выше. Существует 32 вида симметрии, но многие из них имеют очень небольшое значение и редко встречаются среди ми-
неральных образований. В каждой сингонии подавляющее чис-,ло известных представителей обнаруживает степень симметрий! максимально возможную для данной сингонии: они принадлежат к так называемому голоэдрическому виду симметрии данной сингонии. Здесь нам необходимо упомянуть все голоэдрические и только несколько других видов симметрии, в которые попадают важнейшие драгоценные минералы.
I. Триклннная сингония. Голоэдрический класа пинако-идальный. Единственный элемент симметрии — центр симметрии. Общая форма — пинакоид; поскольку каждая форма состоит
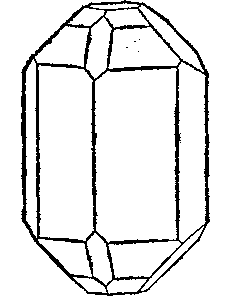
Рис. 22. Кристалл топаза.
Рис, 23. Ромбоэдр,.
из пары параллельных граней, в реальных кристаллах должно существовать не меньше трех таких форм. Этот вид симметрии выражен в плагиоклазах, кианите и родоните.
II.
Моноклинная сингония. Голоэдрический класс, призматический. Элементы симметрии: 1 двойная ось, 1 плоскость (под прямым углом к оси) и центр симметрии.
Особые формы — различные виды пинакоидов, общая форма — призма. Примерно половина всех известных кристаллических веществ относится к этому классу, а среди ювелирных материалов — ортоклаз (рис. 3), сподумен, эвклаз, сфен и эпидот (рис. 20).
III.
Ромбическая сингония. Голоэдрический класс: ромбоби-пирамидальный. Элементы симметрии: 3 взаимно перпендикулярные двойные оси, 3 плоскости (под прямым углом к осям) и центр симметрии.
Особые формы — пинакоиды и призмы; общая форма — бипирамида. По значению этот класс занимает второе меето. К нему принадлежат топаз (рис. 22), оливин и хризоберилл, а также менее известные минералы: андалузит, кордиерит, бериллонит, гам-бергит, данбурит, брукит, фибролит, корнерупин, энетатит и цоизит.
IV.
Тетрагональная сингония. Голоэдрический класа дитетра-гон-бипирамидальный. Элементы симметрии: 1 тетрагональная ось и 4 двойные оси, перпендикулярные ей, 5 плоскостей симметрии (иод прямым углом ко всем осям) и центр симметрии.
Имеется большое количество особых форм; произвольно расположенная грань повторяется в виде четырех пар граней вокруг четверной оси, а они отражаются симметрично в нижней части кристалла, образуя, таким образом, дитетрагональную бипирамиду. Примерами минералов этого класса служат циркон (рис. 2), касситерит и везувиан.
Тетрагон-бипирамидалышй класс. Элементы симметрии: 1 тетрагональная ось, 1 плоскость (под прямым углом к оси) и центр симметрии.
Особые формы — пинакоид (развивающийся из граней, расположенных под прямым углом к оси 4-го порядка) и тетрагональные призмы (из граней, параллельных этой оси); общая форма в этом случае — 8-гранная тетрагональная бипирамида без тех плоскостей симметрии, проходящих через тетрагональную ось, которые создают дитетрагональную симметрию и характерны для голоэдрии. К этому классу относится скаполит, которому иногда придают огранку драгоценного камня.
V.
Гексагональная сингония. Голоэдрический класса дигекса-гон-бипирамидальный. Элементы симметрии: 1 гексагональная ось, 6 двойных осей (под прямым углом к оси 6-го порядка), 7 плоскостей симметрии и центр симметрии.
Этот класс — гексагональный аналог голоэдрического класса тетрагональной сингонии. Среди особых форм фигурируют пина-коиды, призмы и гексагональные бипирамиды; общая форма имеет 6 пар граней, симметрично повторяющихся, что приводит к образованию дигексагональной бипирамиды. Выдающимся представителем этого класса является берилл.
Гексагон-бипирамидалъный класс. Элементы симметрии: 1 ось 6-го порядка, 1 плоскость (под прямым углом к оси) и центр симметрии.
Примером минералов этого класса служит, как уже указывалось, апатит (рис. 18).
VI.
Тригональная сингония. Голоэдрический класс: дитригон-скаленоэдрический. Элементы симметрии: 1 тройная ось, 3 двойные оси, перпендикулярные тройной оси, 3 плоскости (под прямым углом к двойным осям) и центр симметрии.
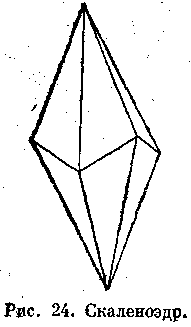
Имеется ряд особых форм, в том числе ромбоэдры (рис. 23). Общая форма, в которой отсутствует горизонтальная плоскость симметрии,— скаленоэдр, а не бипирамида; его название происходит от слова scalene (разносторонний, косой) — по облику неравносторонних треугольных граней (рис. 24). Примеры минералов этого класса — корунд, кальцит и гематит.
Дитригон-пирамидалъный класс. Элементы симметрии: 1 тройная ось и 3 пересекающиеся по ней плоскости.
Особые формы включают как тригональные, так и гексагональные призмы, так что кристаллы могут иметь поперечное сечение в виде равностороннего треугольника. В них нет центра симметрии, общая форма — пирамида (но не бипирамида). Разные концы кристалла имеют различную симметрию. Наиболее наглядным примером минералов этого класса является турмалин (рис. £).
Трйгон-Шрапецоэдрический класс. Элементы симметрии: 1 тройная ось и 3 двойные оси, перпендикулярные тройной оси.
Плоскостей симметрии нет, и в кристаллах этого класса проявляется энантиоморфизм: их общие формы имеют правую и левую модификации, зеркально-симметричные и нееовмещающиеся. К этому классу относится Кварц (рис. 11), обладающий удивительным свойством вращения плоскости поляризации (впервые открытым Араго); это свойство характерно для кристаллов, Лишенных плоскостей симметрии.
Дитригон-бипирамидалъный класс. Элементы симметрии: 1 тройная ось; 3 двойные оси под прямым углом к ней; 3 плоскости, каждая из которых содержит тройную ось и одну из двойных осей, и 1 плоскость, перпендикулярная тройной оси.
Единственным представителем этого класса среди минералов является редкий драгоценный бенитоит.
Ромбоэдрический класс. Элементы симметрии: 1 тройная ось и центр симметрии.
Особые формы: пинакоиды и гексагональные призмы. Общая форма — ромбоэдр. К этому классу относятся фенакит, диоп-таз и виллемит.
VII. Кубическая сингония. Голоэдрический класс: сорокавось-мигранники. Элементы симметрии: 3 оси 4-го порядка, 4 тройные оси, 6 двойных осей; 3 плоскости, расположенные под прямым углом к осям 4-го порядка; 6 других плоскостей (перпендикулярных двойным осям), центр симметрии.
Из особых форм для всех видов симметрии кубической сингонии типичны куб и ромбододекаэдр. Среди других особых форм
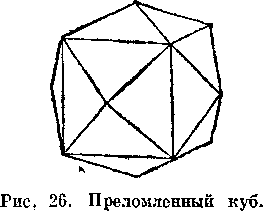
этого класса — октаэдр (рис. 25), преломленный куб (рис. 26), икоситетраэдры и преломленный октаэдр (рис. 27). В кристаллах алмаза иногда четко видна 48-гранная общая форма (сорока-восьмигранник) (рис. 28). Другими примерами минералов этого класса служат гранат, шпинель и флюорит.
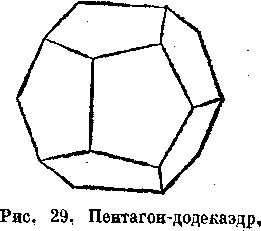
Дидодекаэдрический класс. Элементы симметрии: 3 двойные оси, 4 тройные оси, 3 плоскости (под прямым углом к двойным осям) и центр симметрии.
Характерная особая форма — пентагон-додекаэдр (рис. 29), иногда называемый пиритоэдром, так как он часто хорошо выражен в пирите — одном из главных представителей этого класса.
Класс тетраэдра. Элементы симметрии: 3 двойные оси, 4 тройные оси, 6 плоскостей.
Центра симметрии нет, характерная особая форма — тетраэдр (рис. 5), Примером минералов этого класса служит сфалерит.